A). Difficulties, related to movement (or location) of an object in line are solved, if the object obtains an opportunity to move in two dimensions (i.e. in plane); Correspondingly, the problems related to movement (or location) of objects in a plane are solved with a transition to the space of three dimensions;
B). Use a multi-level composition of objects instead of a single-level one. "Many planes";
C). Incline an object or place it "on its side". "Relocating a plane" (out of orthogonal ways into incline ways). It means out of familiar topology (road) to a new one;
D). Use the opposite side of a given surface. (A plane has two sides!);
E). Use optical flows, falling on the neighboring area or on the opposite side of the existing area;
F). Use transition to another space (and back), from one coordinate system to another;
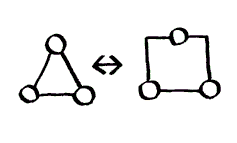
G). Use another structural presentation, i.e. topology, change the order of elements, change combination.

The opposite:
A). Go from many dimensions to fewer ones. For example: making a film, a foil;
B). Use "fewer planes";
C). Make it to the predefined, standard, customary topology. For example: make everything orthogonal;
D). Use only one side of the surface (and use the other side for something else).
Synthesis
There are innumerous examples. Here are some: Fourier transform, Laplace transform, jpeg compression
This is the Method 13 [17] | Index